求解方程根的近似值丨简单迭代法、二分法、牛顿迭代法、弦割法

## 前言
本文章下列内容以解方程

$$e^{x-1}=x+1,x\in(-1,5)$$

为例

函数 $$y=e^{x-1}-x-1$$的图像为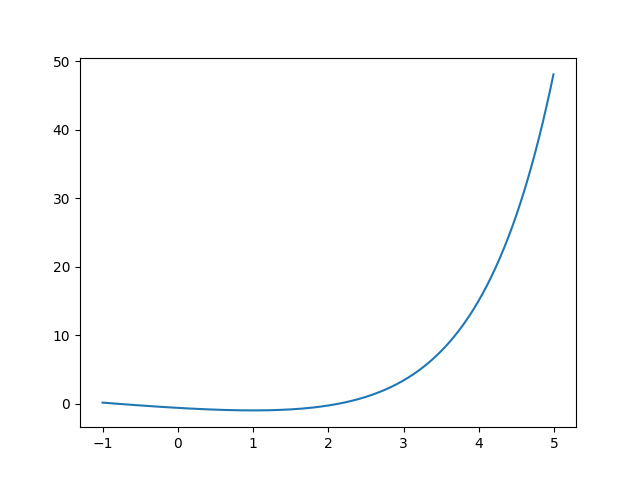

![Figure_1.png](https://picture-1300689095.file.myqcloud.com/2022/12/30/438b26c37346e.png)

前置代码为

```python
import numpy as np
import matplotlib.pyplot as plt

dmin = 1e-10
fmax = 1000

def f(x):
    return np.exp(x - 1) - x - 1

def f_prime(x):
    return np.exp(x - 1) - 1

x = np.arange(-1, 5, 0.01)
y = np.vectorize(f)(x)

rans = []

for i in range(len(y) - 1):
    if (y[i] * y[i + 1] < 0):
        rans.append([x[i], x[i + 1]])

print("该方程共有 " + str(len(rans)) + " 个根")
```

## 简单迭代法
$$f(x) = 0$$

转化为

$$x=g(x)$$

然后进行迭代

$$x_{n+1}=g(x_n)$$

直至收敛

上面的例子中，我们移项可得

$$x_{n+1}=e^{x_n-1}-1$$

```python
def s1mpley(x):
    val = np.exp(x - 1) - 1
    return val

def s1mple(x, num):
    x0 = s1mpley(x)
    if (abs(x - x0) <= dmin or num > fmax):
        return [x, num]
    else:
        return s1mple(x0, num + 1)

for i in range(len(rans)):
    s1mple_ans = s1mple(rans[i][0], 0)
    print("第 ", i + 1, " 个根：", s1mple_ans)
```

但之后，简单迭代法只能计算出一个根，这和所取的迭代方程有关

```python
该方程共有 2 个根
第  1  个根： [-0.8414056605230351, 10]
第  2  个根： [-0.841405660391821, 19]
```

## 二分法
简单粗暴，有根的区间的长度<精度后，只需要取左端点即可

```python
def er(a, b, num):
    x0 = (a + b) / 2
    val = np.vectorize(f)(x0)
    if (val == 0):
        return [x0, num]
    else:
        if (val < 0):
            a = x0
        else:
            b = x0
    if (abs(b - a) <= dmin or num > fmax):
        return [x0, num]
    else:
        return er(a, b, num + 1)

for i in range(len(rans)):
    er_ans = er(rans[i][0], rans[i][1], 0)
    print("第 ", i + 1, " 个根：", er_ans)
```

二分法成功计算出了两个根，但迭代次数很多，在提前缩短区间长度后仍然很多
```python
该方程共有 2 个根
第  1  个根： [-0.8499999999254941, 26]
第  2  个根： [2.146193220689896, 26]
```

## 牛顿迭代法
$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$

```python
def newtony(x):
    val = f(x) / f_prime(x)
    return val

def newton(x, num):
    x0 = x - newtony(x)
    if (abs(x - x0) <= dmin or num > fmax):
        return [x, num]
    else:
        return newton(x0, num + 1)

for i in range(len(rans)):
    newton_ans = newton(rans[i][0], 0)
    print("第 ", i + 1, " 个根：", newton_ans)
```

~~快如闪电~~
在提前求导的前提下，牛顿迭代法的收敛速度特别的快
```python
该方程共有 2 个根
第  1  个根： [-0.8414056604414608, 2]
第  2  个根： [2.1461932206205825, 3]
```

## 弦割法

$$
x_{n+1}=x_n-\dfrac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}f(x_n)
$$

牛顿迭代法的改良版本

不知道导数怎么办，没关系，我们可以用两点间的线的斜率代替导数

```python
def xiany(a, b):
    val = (a - b) / (f(a) - f(b)) * f(a)
    return val

def xian(a, b, num):
    x0 = a - xiany(a, b)
    if (abs(a - x0) <= dmin or num > fmax):
        return [x0, num]
    else:
        return xian(x0, a, num + 1)

for i in range(len(rans)):
    xian_ans = xian(rans[i][0], rans[i][1], 0)
    print("第 ", i + 1, " 个根：", xian_ans)
```

同样很快，而且适用性更广
```python
该方程共有 2 个根
第  1  个根： [-0.8414056604369607, 3]
第  2  个根： [2.1461932206205825, 3]
```

求解方程根的近似值丨简单迭代法、二分法、牛顿迭代法、弦割法

添加新评论

轻语

最新文章

最近回复

分类

标签

归档

其它